4-1-  المعدلات المتكافئة (ساحل، 2017) :

      يكون معدلين لفترتين مختلفتين متكافئتين، إذا أنتجا نفس القيمة المكتسبة أو الجملة بنفس رأس المال و لنفس الفترة.

و بصفة عامة إذا كان t_a: معدل الفائدة السنوي و لفترة واحدة، و t_k هو معدل الموافق للفترة q و م هي جزء من الفترة الواحدة. فإن t_k و   t_k يكونا متكافئتين إذا كان لدينا:

C(1+t_a) = c(1+t_k)^q

(1+t_a) = (1+t_k)^q

ملاحظة: المعدل المكافئ يطبق في حالة الفائدة المركبة.

مثال(3-13):

        ما هو  المعدل السداسي المكافئ للمعدل السنوي 9%.

الحل:

q=2              t_a= 9%

 (1+t_a) = (1+t_s)^q  (1+0.09) = (1+t_s)²

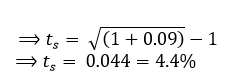
تمرين

أودع شخص في أحد البنوك و بمعدل فائدة مركبة سنوي 5,5% المبالغ التالية:

-       1800 دج في 01-01-2002.

-       2300 دج في 01-01-2003.

-       970 دج في 01-01-2004.

المطلوب: أحسب المبلغ الإجمالي المسحوب في 01-01-2006.

الحل:

  المبلغ الإجمالي المسحوب يمثل جملة المبالغ الثلاثة المودعة إلى غاية 01-01-2006:

C_nTotal= 1800(1+0.055) ⁴+2300(1+0.055) ³ +970(1+0.055) ² = 6010.26 DA